Gabriel Cramer
nacido en Ginebra (Suiza) en 1704, fue
un matemático precoz que obtuvo el doctorado a los 18 años de edad.
Fue profesor y catedrático de la Universidad de Ginebra y entre sus obras
destaca Introducción al análisis de las curvas algebraicas (1950),
donde clasifica las curvas según el grado de las ecuaciones.
Es en esta obra donde reintroduce el concepto de determinantes de
Leibniz (1646) y presenta el teorema ahora conocido, en su honor, como Regla
de Cramer.
Este teorema, la Regla de Cramer, permite, mediante la
aplicación de la función determinante, la obtención
inmediata de la solución de los Sistemas de Ecuaciones
Compatibles Determinados, como veremos más adelante.
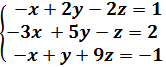
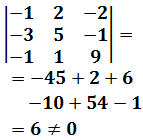
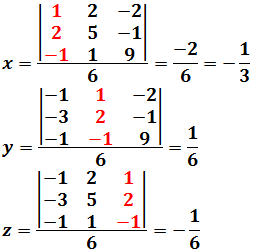
Dado un sistema de ecuaciones lineales (SEL) con tantas ecuaciones como incógnitas, si la matriz coeficientes del sistema es regular (las ecuaciones son linealmente independientes), podemos obtener la única solución del sistema calculando determinantes (tantos como el número de incógnitas).
El valor de la incógnita correspondiente a una determinada columna del sistema viene dado por el determinante de la matriz que se obtiene al sustituir la columna de la dicha incógnita por la columna de los términos independientes y dividiendo este resultado por el determinante de la matriz coeficientes.
Por tanto, la regla de Cramer es de gran utilidad ya que podemos calcular la solución de un sistema compatible determinado rápidamente.
Recordemos que...
-
La matriz de coeficientes ha de ser necesariamente regular.
-
Si el vector de términos independientes está formado únicamente por ceros (sistema homogéneo), no es necesario aplicar la regla ya que cada determinante tendrá una columna de ceros y, por tanto, obtendremos un 0. En efecto, la solución es la solución ceros.
- No olvidar que el sistema debe estar ordenado: cada columna tiene que estar formada por los coeficientes en cada ecuación de una misma incógnita
Si la matriz no es regular (es singular), el sistema no es compatible determinado. El sistema será o bien indeterminado, o bien incompatible. En el primer caso no podemos aplicar Cramer; en el segundo, no hay solución.
Ejemplo:
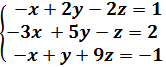
El determinante de la matriz es
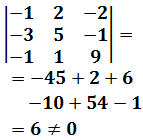
Por tanto, la matriz es regular y el sistema tiene una única solución. Aplicamos la regla de Cramer para obtener la solución:
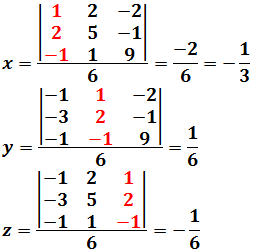
No hay comentarios:
Publicar un comentario